본문으로 이동

FDTD법

위키백과, 우리 모두의 백과사전.
유한차분 시간영역법에서 "이 격자"는 맥스웰 방정식을 공간에서 이산화하는 데 사용된다. 이 방법은 전기장과 자기장을 지그재그식 격자에 배치하는 것을 포함한다.

FDTD법, 풀어서 유한차분 시간영역법(Finite-difference time-domain method) 또는 이 방법(Yee lattice, 케인 S. 이, 1934년생 중국계 미국인 응용 수학자의 이름을 따서 명명됨)은 전산 전자기학을 모델링하는 데 사용되는 수치해석학 기술이다.

역사

[편집]

시간 의존적 편미분 방정식에 대한 유한차분 기법은 전산 유체 역학 문제에서 수년 동안 사용되어 왔으며,[1] 2차 정확도를 달성하기 위해 공간 및 시간에서 엇갈린 격자에 중심 유한차분 연산자를 사용하는 아이디어를 포함한다.[1] 1966년 그의 중요한 논문에서 제시된 이의 FDTD 기법의 참신함은 맥스웰의 회전 방정식에서 각 전기장 및 자기장 벡터 성분에 대해 공간 및 시간에서 엇갈린 격자에 중심 유한차분 연산자를 적용하는 것이었다.[2] "유한차분 시간영역"이라는 명칭과 그에 해당하는 "FDTD" 약어는 1980년 앨런 태플로브에 의해 시작되었다.[3] 1990년경부터 FDTD 기법은 재료 구조와 전자기파 상호작용을 다루는 많은 과학 및 공학 문제를 전산적으로 모델링하는 주요 수단으로 부상했다. 현재 FDTD 모델링 응용 분야는 거의 직류 (지구-전리층 도파관 전체를 포함하는 초저주파 지구물리학)부터 마이크로파 (레이더 신호 기술, 안테나, 무선 통신 장치, 디지털 상호 연결, 생체 의학 영상/치료)를 거쳐 가시광선 (광결정, 나노플라스몬, 솔리톤 및 생체 광학)에 이른다.[4] 2006년에는 과학 및 공학 문헌에 약 2,000건의 FDTD 관련 출판물이 등장했다 (참고: 인기). 2013년 기준으로, 최소 25개의 상용/독점 FDTD 소프트웨어 공급업체, 13개의 자유 소프트웨어/오픈 소스 소프트웨어 FDTD 프로젝트, 그리고 2개의 프리웨어/클로즈드 소스 FDTD 프로젝트가 있으며, 일부는 상업적 용도로 사용되지 않는다 (참고: 외부 링크).

FDTD 및 맥스웰 방정식의 개발

[편집]

맥스웰 방정식에 대한 FDTD 수치 기법의 기초, 기술 개발 및 가능한 미래에 대한 이해는 먼저 그 역사를 고려함으로써 개발될 수 있다. 다음은 이 분야의 주요 출판물 중 일부를 나열한다.

맥스웰 방정식에 대한 FDTD 기법 및 응용의 부분 연대기[5]
연도 사건
1928 Courant, Friedrichs, Lewy (CFL)는 명시적 시간 의존적 유한차분 기법의 조건부 안정성 발견에 대한 중요한 논문을 발표하고, 1차원 및 2차원 2차 파동 방정식을 푸는 고전적인 FD 기법을 발표했다.[6]
1950 암시적/명시적 시간 의존적 유한차분법에 대한 폰 노이만 안정성 분석 방법의 첫 등장.[7]
1966 Yee는 공간과 시간에서 엇갈린 격자에서 맥스웰의 회전 방정식을 풀기 위한 FDTD 수치 기법을 설명했다.[2]
1969 Lam은 폰 노이만 안정성 분석을 사용하여 이의 알고리즘에 대한 정확한 수치 CFL 안정성 조건을 보고했다.[8]
1975 Taflove와 Brodwin은 재료 구조와 2차원 및 3차원 전자기파 상호작용에 대한 최초의 정현파 정상 상태 FDTD 해를 보고했으며,[9] 최초의 생체 전자기학 모델을 보고했다.[10]
1977 Holland와 Kunz & Lee는 EMP 문제에 이의 알고리즘을 적용했다.[11][12]
1980 Taflove는 FDTD 약어를 만들고 3차원 금속 공동으로의 정현파 정상 상태 전자기파 침투에 대한 최초의 검증된 FDTD 모델을 발표했다.[3]
1981 Mur는 이의 격자에 대한 최초의 수치적으로 안정적이고 2차 정확한 흡수 경계 조건(ABC)을 발표했다.[13]
1982–83 Taflove와 Umashankar는 2차원 및 3차원 구조에 대한 정현파 정상 상태 근거리장, 원거리장 및 레이더 단면적을 계산하는 최초의 FDTD 전자기파 산란 모델을 개발했다.[14][15]
1984 Liao 등은 외부 격자 경계에 인접한 필드의 시공간 외삽법을 기반으로 하는 개선된 ABC를 보고했다.[16]
1985 Gwarek는 FDTD의 집중 등가 회로 공식을 도입했다.[17]
1986 Choi와 Hoefer는 도파관 구조의 최초 FDTD 시뮬레이션을 발표했다.[18]
1987–88 Kriegsmann 등과 Moore 등은 IEEE Transactions on Antennas and Propagation에 ABC 이론에 대한 첫 논문을 발표했다.[19][20]
1987–88, 1992 Umashankar 등이 가는 전선 및 전선 묶음의 FDTD 모델링을 허용하기 위해 윤곽 경로 하위 셀 기법을 도입했으며,[21] Taflove 등이 전도성 스크린의 균열을 통한 침투를 모델링하기 위해,[22] 그리고 Jurgens 등이 부드럽게 곡선된 산란체의 표면을 등각적으로 모델링하기 위해 도입했다.[23]
1988 Sullivan 등은 완전한 인체에 의한 정현파 정상 상태 전자기파 흡수에 대한 최초의 3D FDTD 모델을 발표했다.[24]
1988 Zhang 등이 마이크로스트립의 FDTD 모델링을 도입했다.[25]
1990–91 Kashiwa와 Fukai,[26] Luebbers 등,[27] 그리고 Joseph 등이 주파수 의존 유전율의 FDTD 모델링을 도입했다.[28]
1990–91 Maloney 등,[29] Katz 등,[30] 그리고 Tirkas와 Balanis가 안테나의 FDTD 모델링을 도입했다.[31]
1990 Sano와 Shibata,[32] 그리고 El-Ghazaly 등이 피코초 광전자 스위치의 FDTD 모델링을 도입했다.[33]
1992–94 비선형 분산 매체에서 광학 펄스 전파의 FDTD 모델링이 도입되었으며, Goorjian과 Taflove에 의한 1차원 최초의 시간적 솔리톤;[34] Ziolkowski와 Judkins에 의한 빔 자기 초점;[35] Joseph 등에 의한 2차원 최초의 시간적 솔리톤;[36] 그리고 Joseph와 Taflove에 의한 2차원 최초의 공간적 솔리톤을 포함한다.[37]
1992 Sui 등이 집중 전자 회로 요소의 FDTD 모델링을 도입했다.[38]
1993 Toland 등은 공동 및 안테나를 여기시키는 이득 장치(터널 다이오드 및 건 다이오드)의 최초 FDTD 모델을 발표했다.[39]
1993 Aoyagi 등은 하이브리드 이 알고리즘/스칼라파 방정식과 이 스킴과 전자기파 방정식에 대한 유한차분 스킴의 등가성을 입증했다.[40]
1994 Thomas 등은 FDTD 공간 격자에 대한 노턴 등가 회로를 도입하여 SPICE 회로 분석 도구가 격자에 내장된 비선형 전자 부품 또는 완전한 회로의 정확한 하위 격자 모델을 구현할 수 있도록 했다.[41]
1994 Berenger는 2차원 FDTD 격자를 위한 매우 효과적인 완전 일치층(PML) ABC를 도입했으며,[42] 이는 Navarro 등이 비직교 메시로,[43] Katz 등이 3차원으로,[44] 그리고 Reuter 등이 분산 도파관 종단으로 확장했다.[45]
1994 Chew와 Weedon은 3차원, 다른 좌표계 및 다른 물리 방정식으로 쉽게 확장될 수 있는 좌표 확장 PML을 도입했다.[46]
1995–96 Sacks 등과 Gedney는 물리적으로 실현 가능한 단축 완전 일치층(UPML) ABC를 도입했다.[47][48]
1997 Liu는 나이퀴스트 한계에서 전자기장을 극히 거친 공간 샘플링을 허용하는 유사 스펙트럼 시간 영역(PSTD) 방법을 도입했다.[49]
1997 Ramahi는 매우 효과적인 해석적 ABC를 구현하기 위해 보완 연산자 방법(COM)을 도입했다.[50]
1998 Maloney와 Kesler는 FDTD 공간 격자에서 주기적 구조를 분석하는 몇 가지 새로운 방법을 도입했다.[51]
1998 Nagra와 York는 여러 에너지 준위 사이를 전이하는 전자를 가진 재료와 전자기파 상호작용에 대한 하이브리드 FDTD-양자 역학 모델을 도입했다.[52]
1998 Hagness 등은 초광대역 레이더 기술을 사용한 유방암 탐지에 대한 FDTD 모델링을 도입했다.[53]
1999 Schneider와 Wagner는 복소수 파수를 기반으로 한 FDTD 격자 분산의 포괄적인 분석을 도입했다.[54]
2000–01 Zheng, Chen, Zhang은 증명 가능한 무조건적인 수치 안정성을 가진 최초의 3차원 교번 방향 암시적(ADI) FDTD 알고리즘을 도입했다.[55][56]
2000 Roden과 Gedney는 고급 합성 PML(CPML) ABC를 도입했다.[57]
2000 Rylander와 Bondeson은 증명 가능하게 안정적인 FDTD - 유한요소 시간 영역 하이브리드 기법을 도입했다.[58]
2002 Hayakawa 등과 Simpson과 Taflove는 극저주파 지구물리학적 현상에 대한 지구-전리층 도파관의 FDTD 모델링을 독립적으로 도입했다.[59][60]
2003 DeRaedt는 무조건적으로 안정적인 "원스텝" FDTD 기법을 도입했다.[61]
2004 Soriano와 Navarro는 양자 FDTD 기법에 대한 안정성 조건을 도출했다.[62]
2008 Ahmed, Chua, Li, Chen은 3차원 국부적 1차원(LOD)FDTD 방법을 도입하고 무조건적인 수치 안정성을 입증했다.[63]
2008 Taniguchi, Baba, Nagaoka, Ametani는 전도성 매체에 대한 FDTD 계산을 위한 가는 선 표현을 도입했다.[64]
2009 Oliveira와 Sobrinho는 전력 변전소에서 낙뢰를 시뮬레이션하기 위해 FDTD 방법을 적용했다.[65]
2021 Oliveira와 Paiva는 FDTD CFL 한계를 넘어 시간 단계를 사용하기 위한 최소 제곱 유한차분 시간 영역 방법(LS-FDTD)을 개발했다.[66]

FDTD 모델 및 방법

[편집]

맥스웰 미분 방정식을 살펴보면, 시간 내 E-장 변화(시간 미분)가 공간 내 H-장 변화(회전)에 의존한다는 것을 알 수 있다. 이로 인해 FDTD 시간 스텝 관계가 기본적으로 성립하는데, 이는 공간의 어느 지점에서든 시간에 따른 E-장의 업데이트된 값이 E-장의 저장된 값과 공간 내 H-장의 국부 분포에 대한 수치적 회전에 의존한다는 것이다.[2]

H-장도 유사한 방식으로 시간 스텝을 밟는다. 공간의 어느 지점에서든 시간에 따른 H-장의 업데이트된 값은 H-장의 저장된 값과 공간 내 E-장의 국부 분포에 대한 수치적 회전에 의존한다. E-장 및 H-장 업데이트를 반복하면 컴퓨터 메모리에 저장된 수치 격자에서 고려 중인 연속적인 전자기파의 샘플링 데이터 아날로그가 전파되는 시간 진행 과정이 발생한다.

FDTD에 사용되는 표준 직교 이 셀의 그림으로, 전기장 및 자기장 벡터 성분이 분포되어 있다.[2] 입방형 복셀로 시각화하면, 전기장 성분은 입방체의 모서리를 형성하고 자기장 성분은 입방체의 면에 대한 법선을 형성한다. 3차원 공간 격자는 이러한 이 셀의 다중으로 구성된다. 전자기파 상호작용 구조는 각 전기장 성분에는 적절한 유전율 값을 할당하고 각 자기장 성분에는 투자율을 할당하여 공간 격자로 매핑된다.

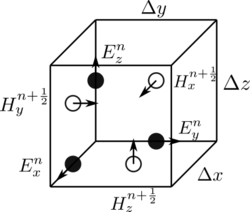
이 설명은 1차원, 2차원 및 3차원 FDTD 기법에 모두 해당된다. 여러 차원을 고려할 때 수치적 회전을 계산하는 것은 복잡해질 수 있다. 케인 이의 1966년 선구적인 논문은 직교 좌표 계산 격자의 직사각형 단위 셀 주위에 E-장 및 H-장 벡터 성분을 공간적으로 엇갈리게 배치하여 각 E-장 벡터 성분이 한 쌍의 H-장 벡터 성분 사이에 중간에 위치하도록 제안했다.[2] 현재 이 격자로 알려진 이 방법은 매우 견고한 것으로 입증되었으며, 많은 현재 FDTD 소프트웨어 구성의 핵심으로 남아 있다.

또한 이(Yee)는 E-장과 H-장의 업데이트가 엇갈리게 진행되는 도약 방식을 제안했다. 즉, E-장 업데이트는 연속적인 H-장 업데이트 사이의 각 시간 단계 중간에 수행되고, 그 반대도 마찬가지이다.[2] 장점으로는 이 명시적 시간 진행 방식은 동시 방정식을 풀 필요를 피하며, 또한 소산 없는 수치적 파동 전파를 제공한다. 단점으로는 이 방식은 수치적 안정성을 보장하기 위해 시간 단계에 상한선을 요구한다.[9] 결과적으로 특정 유형의 시뮬레이션은 완료하는 데 수천 번의 시간 단계가 필요할 수 있다.

FDTD 방법 사용

[편집]

맥스웰 방정식의 FDTD 해를 구현하려면 먼저 계산 영역을 설정해야 한다. 계산 영역은 시뮬레이션이 수행될 물리적 영역을 의미한다. E-장과 H-장은 해당 계산 영역 내 공간의 모든 지점에서 결정된다. 계산 영역 내 각 셀의 재료를 지정해야 한다. 일반적으로 재료는 자유 공간(공기), 금속 또는 유전체이다. 투자율, 유전율 및 도전율이 지정되는 한 어떤 재료도 사용할 수 있다.

테이블 형식의 분산 재료의 유전율은 FDTD 방식에 직접 대입할 수 없다. 대신, 여러 데바이, 드루데, 로렌츠 또는 임계점 항을 사용하여 근사할 수 있다. 이 근사는 개방형 피팅 프로그램을 사용하여 얻을 수 있으며[67] 반드시 물리적 의미를 가질 필요는 없다.

계산 영역과 격자 재료가 설정되면 소스가 지정된다. 소스는 전선 위의 전류, 인가된 전기장 또는 입사 평면파가 될 수 있다. 후자의 경우 FDTD는 임의 모양의 물체, 다양한 입사각에서의 평면 주기 구조,[68][69] 및 무한 주기 구조의 광자 밴드 구조로부터의 빛 산란을 시뮬레이션하는 데 사용될 수 있다.[70][71]

E-장과 H-장이 직접 결정되므로 시뮬레이션의 출력은 일반적으로 계산 영역 내의 한 점 또는 일련의 점에서의 E-장 또는 H-장이다. 시뮬레이션은 E-장과 H-장을 시간적으로 앞으로 진행시킨다.

시뮬레이션에서 반환된 E-장과 H-장에 대한 처리가 수행될 수 있다. 데이터 처리는 시뮬레이션이 진행되는 동안에도 발생할 수 있다.

FDTD 기술은 압축된 공간 영역 내에서 전자기장을 계산하지만, 산란 및 방사된 원거리장은 근거리-원거리장 변환을 통해 얻을 수 있다.[14]

안정성

[편집]

FDTD 방법의 선형성 때문에 FDTD 방법의 안정성 영역은 폰 노이만 안정성 분석에 의해 결정될 수 있다. 이 방법은 전기장과 자기장이 단색 복소수 지수에 비례한다고 가정한다. 단일 시간 단계 후에 안정적인 장의 진폭 크기는 같거나 작게 유지되어야 한다. 이는 FDTD 매개변수 간의 관계를 설명하여 안정성을 보장하는 코란트-프리드리히-레비 조건으로 이어진다.[4]

FDTD 모델링의 장점

[편집]

모든 모델링 기법에는 장점과 단점이 있으며, FDTD 방법도 다르지 않다.

  • FDTD는 맥스웰 방정식을 푸는 데 사용되는 다목적 모델링 기법이다. 직관적이기 때문에 사용자가 쉽게 사용 방법을 이해하고 주어진 모델에서 무엇을 기대해야 하는지 알 수 있다.
  • FDTD는 시간 영역 기법이며, 광대역 펄스(예: 가우스 펄스)를 소스로 사용하면 단일 시뮬레이션으로 넓은 주파수 범위에 걸쳐 시스템의 응답을 얻을 수 있다. 이는 공진 주파수가 정확히 알려지지 않았거나 광대역 결과가 필요한 모든 응용 분야에서 유용하다.
  • FDTD는 계산 영역의 모든 지점에서 시간에 따라 E 및 H 필드를 계산하므로, 모델을 통해 전자기장 이동의 애니메이션 표시를 제공하는 데 적합하다. 이러한 유형의 표시는 모델에서 무슨 일이 일어나고 있는지 이해하고 모델이 올바르게 작동하는지 확인하는 데 유용하다.
  • FDTD 기술을 통해 사용자는 계산 영역 내의 모든 지점에서 재료를 지정할 수 있다. 다양한 선형 및 비선형 유전체 및 자기 재료를 자연스럽고 쉽게 모델링할 수 있다.
  • FDTD는 조리개의 효과를 직접 결정할 수 있다. 차폐 효과를 찾을 수 있으며, 구조 내부 및 외부의 필드를 직접 또는 간접적으로 찾을 수 있다.
  • FDTD는 E-장과 H-장을 직접 사용한다. 대부분의 EMI/EMC 모델링 응용 프로그램이 E-장과 H-장에 관심이 있으므로 시뮬레이션이 실행된 후 이러한 값을 얻기 위해 변환을 할 필요가 없다는 점이 편리하다.

FDTD 모델링의 단점

[편집]
간단한 1차원 FDTD 방식에서 사각 펄스 신호의 수치적 분산. 펄스 가장자리 주변의 링잉 아티팩트가 심하게 강조되고 (깁스 현상) 신호는 분산 매체가 없는 경우에도 전파되면서 왜곡된다. 이 아티팩트는 이산화 방식의 직접적인 결과이다.[4]
  • FDTD는 전체 계산 영역이 격자로 분할되어야 하고, 격자 공간 이산화가 모델에서 가장 작은 전자기 파장과 가장 작은 기하학적 특징을 모두 해결할 수 있을 만큼 충분히 미세해야 하므로, 매우 큰 계산 영역이 개발될 수 있으며, 이는 매우 긴 해결 시간으로 이어진다. 길고 가는 특징(예: 전선)을 가진 모델은 과도하게 큰 계산 영역이 필요하기 때문에 FDTD에서 모델링하기 어렵다. 고유모드 확장과 같은 방법은 Z 방향을 따라 미세한 격자가 필요하지 않으므로 더 효율적인 대안을 제공할 수 있다.[72]
  • 재료 인터페이스에서 유전율과 투자율에 대한 고유한 값을 결정할 방법이 없다.
  • 공간 및 시간 단계는 CFL 조건을 충족해야 하며, 그렇지 않으면 편미분 방정식을 푸는 데 사용되는 도약적분이 불안정해질 가능성이 있다.
  • FDTD는 계산 영역의 모든 곳에서 E/H 필드를 직접 찾는다. 일부 거리에서 필드 값이 필요한 경우, 이 거리는 계산 영역을 지나치게 크게 만들 수 있다. FDTD에 대한 원거리장 확장이 가능하지만, 약간의 후처리가 필요하다.[4]
  • FDTD 시뮬레이션은 계산 영역 내의 모든 지점에서 E 및 H 필드를 계산하므로, 컴퓨터 메모리에 상주할 수 있도록 계산 영역은 유한해야 한다. 많은 경우 이는 시뮬레이션 공간에 인공 경계를 삽입함으로써 달성된다. 이러한 경계에 의해 발생하는 오류를 최소화하기 위해 주의를 기울여야 한다. 무한한 무경계 계산 영역을 시뮬레이션하기 위한 여러 가지 매우 효과적인 흡수 경계 조건(ABC)이 있다.[4] 대부분의 현대 FDTD 구현은 대신 흡수 경계를 구현하기 위해 완전 일치층 (PML)이라는 특수 흡수 "재료"를 사용한다.[42][47]
  • FDTD는 시간 영역에서 필드를 앞으로 전파함으로써 해결되므로, 매질의 전자기 시간 응답을 명시적으로 모델링해야 한다. 임의의 응답의 경우, 이는 계산적으로 비용이 많이 드는 시간 컨볼루션을 포함하지만, 대부분의 경우 매질의 시간 응답(또는 분산 (광학))은 재귀 컨볼루션(RC) 기술, 보조 미분 방정식(ADE) 기술 또는 Z-변환 기술을 사용하여 적절하고 간단하게 모델링할 수 있다. 임의의 분산을 쉽게 처리할 수 있는 유사 스펙트럼 공간 영역 (PSSD)은 대신 필드를 공간적으로 앞으로 전파한다.

격자 절단 기술

[편집]

개방 영역 FDTD 모델링 문제에 가장 일반적으로 사용되는 격자 절단 기술은 Mur 흡수 경계 조건(ABC),[13] Liao ABC,[16] 및 다양한 완전 일치층 (PML) 공식이다.[4][43][42][47] Mur 및 Liao 기술은 PML보다 간단하다. 그러나 PML(엄밀히 말하면 경계 조건이라기보다는 흡수 영역)은 몇 배 더 낮은 반사를 제공할 수 있다. PML 개념은 J.-P. Berenger가 1994년 Journal of Computational Physics에 실린 선구적인 논문에서 소개했다.[42] 1994년 이후 Berenger의 원래 분리 필드 구현은 단축 PML(UPML), 컨볼루션 PML(CPML) 및 고차 PML로 수정 및 확장되었다. 후자의 두 PML 공식은 소멸파를 흡수하는 능력이 향상되었으므로, 원칙적으로 Berenger의 원래 공식보다 시뮬레이션된 산란 또는 복사 구조에 더 가깝게 배치될 수 있다.

PML로부터의 원치 않는 수치 반사를 줄이기 위해 추가적인 후방 흡수층 기술을 사용할 수 있다.[73]

인기

[편집]

동일 기간 동안 학술 출판 처리량의 일반적인 증가와 모든 수치 전자기학 (CEM) 기술에 대한 전반적인 관심 확대에도 불구하고, 맥스웰 방정식에 대한 FDTD 전산 해법 접근 방식에 대한 엄청난 관심 확대에는 일곱 가지 주요 이유가 있다.

  1. FDTD는 행렬 역변환을 요구하지 않는다. 완전히 명시적인 계산이므로, FDTD는 주파수 영역 적분 방정식 및 유한요소 전자기학 모델의 크기를 일반적으로 109개 미만의 전자기장 미지수로 제한하는 행렬 역변환의 어려움을 피한다.[4] 109개만큼 많은 필드 미지수를 가진 FDTD 모델이 실행되었으며, 이 수치에는 본질적인 상한이 없다.[4]
  2. FDTD는 정확하고 견고하다. FDTD 계산의 오류 원인은 잘 이해되어 있으며, 매우 다양한 전자기파 상호작용 문제에 대한 정확한 모델을 허용하도록 제한될 수 있다.[4]
  3. FDTD는 충격적인 동작을 자연스럽게 처리한다. 시간 영역 기술이므로, FDTD는 전자기 시스템의 충격 응답을 직접 계산한다. 따라서 단일 FDTD 시뮬레이션은 여기 스펙트럼 내의 모든 주파수에서 초광대역 시간 파형 또는 정현파 정상 상태 응답을 제공할 수 있다.[4]
  4. FDTD는 비선형 동작을 자연스럽게 처리한다. 시간 영역 기술이므로, FDTD는 전자기 시스템의 비선형 응답을 직접 계산한다. 이를 통해 FDTD와 고전적 또는 반고전적 관점에서 비선형성을 설명하는 보조 미분 방정식 세트를 자연스럽게 결합할 수 있다.[4] 한 가지 연구 분야는 FDTD 고전 전자기학 모델과 양자 전자기학에서 발생하는 현상, 특히 카시미르 효과와 같은 진공 요동을 결합하는 하이브리드 알고리즘의 개발이다.[4][74]
  5. FDTD는 체계적인 접근 방식이다. FDTD를 사용하면 모델링할 새로운 구조를 지정하는 것이 적분 방정식의 잠재적으로 복잡한 재구성보다는 메시 생성 문제로 축소된다. 예를 들어, FDTD는 구조 의존적 그린 함수의 계산을 요구하지 않는다.[4]
  6. 병렬 처리 컴퓨터 아키텍처가 슈퍼컴퓨팅을 지배하게 되었다. FDTD는 병렬 처리 CPU 기반 컴퓨터에서 높은 효율성으로 확장되며, 최근 개발된 GPU 기반 가속기 기술에서 매우 잘 작동한다.[4]
  7. 컴퓨터 시각화 기능이 빠르게 증가하고 있다. 이러한 추세는 모든 수치 기법에 긍정적인 영향을 미치지만, 필드 동역학을 설명하는 데 적합한 시간 진행 필드 양의 배열을 생성하는 FDTD 방법에는 특히 유리하다.[4]
  8. 이방성은 FDTD 방법으로 자연스럽게 처리된다. 각 직교 방향에 성분을 갖는 이(Yee) 셀은 이방성 특성으로 쉽게 구성될 수 있다.[4]

태플로브는 이러한 요소들이 결합하여 FDTD가 지배적인 전산 전자기학 기술 중 하나로 남을 것임을 시사한다고 주장했다 (다른 다중 물리 문제에서도 마찬가지이다).[4]

같이 보기

[편집]

각주

[편집]
  1. ↑ 가 나 J. von Neumann; RD Richtmyer (March 1950). 《A method for the numerical calculation of hydrodynamic shocks》. 《Journal of Applied Physics》 21. 232–237쪽. Bibcode:1950JAP....21..232V. doi:10.1063/1.1699639. 
  2. ↑ 가 나 다 라 마 바 Kane Yee (1966). 《Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media》. 《IEEE Transactions on Antennas and Propagation》 14. 302–307쪽. Bibcode:1966ITAP...14..302Y. doi:10.1109/TAP.1966.1138693. S2CID 122712881. 
  3. ↑ 가 나 A. Taflove (1980). 《Application of the finite-difference time-domain method to sinusoidal steady state electromagnetic penetration problems》 (PDF). 《IEEE Trans. Electromagn. Compat.》 22. 191–202쪽. Bibcode:1980ITElC..22..191T. doi:10.1109/TEMC.1980.303879. S2CID 39236486. 
  4. ↑ 가 나 다 라 마 바 사 아 자 차 카 타 파 하 거 너 더 앨런 태플로브 and 수잔 C. 해그니스 (2005). 《Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.》. Artech House Publishers. ISBN 978-1-58053-832-9. 
  5. ↑ Taflove and Hagness (2005)의 허가를 받아 각색.
  6. ↑ Richard Courant; Kurt Otto Friedrichs; Hans Lewy (1928). 《Über die partiellen Differenzengleichungen der mathematischen Physik》 (독일어). 《Mathematische Annalen》 100. 32–74쪽. Bibcode:1928MatAn.100...32C. doi:10.1007/BF01448839. JFM 54.0486.01. MR 1512478. S2CID 120760331. 
  7. ↑ G. G. O’Brien, M. A Hyman, and S. Kaplan (1950). 《A study of the numerical solution of partial differential equations》. 《Journal of Mathematical Physics》 29. 223–251쪽. doi:10.1002/sapm1950291223. MR 0040805. 
  8. ↑ Dong-Hoa Lam (1969). 《Finite Difference Methods for Electromagnetic Scattering Problems》 (PDF). 《Mississippi State University, Interaction Notes》 44. 
  9. ↑ 가 나 A. Taflove; M. E. Brodwin (1975). 《Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell's equations》 (PDF). 《IEEE Transactions on Microwave Theory and Techniques》 23. 623–630쪽. Bibcode:1975ITMTT..23..623T. doi:10.1109/TMTT.1975.1128640. 
  10. ↑ A. Taflove; M. E. Brodwin (1975). 《Computation of the electromagnetic fields and induced temperatures within a model of the microwave-irradiated human eye》 (PDF). 《IEEE Transactions on Microwave Theory and Techniques》 23. 888–896쪽. Bibcode:1975ITMTT..23..888T. doi:10.1109/TMTT.1975.1128708. 
  11. ↑ R. Holland (1977). 《Threde: A free-field EMP coupling and scattering code》. 《IEEE Transactions on Nuclear Science》 24. 2416–2421쪽. Bibcode:1977ITNS...24.2416H. doi:10.1109/TNS.1977.4329229. S2CID 35395821. 
  12. ↑ K. S. Kunz; K. M. Lee (1978). 《A three-dimensional finite-difference solution of the external response of an aircraft to a complex transient EM environment》. 《IEEE Trans. Electromagn. Compat.》 20. 333–341쪽. doi:10.1109/TEMC.1978.303727. S2CID 31666283. 
  13. ↑ 가 나 G. Mur (1981). 《Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic field equations》. 《IEEE Trans. Electromagn. Compat.》 23. 377–382쪽. doi:10.1109/TEMC.1981.303970. S2CID 25768246. 
  14. ↑ 가 나 K. R. Umashankar; A. Taflove (1982). 《A novel method to analyze electromagnetic scattering of complex objects》 (PDF). 《IEEE Trans. Electromagn. Compat.》 24. 397–405쪽. Bibcode:1982ITElC..24..397U. doi:10.1109/TEMC.1982.304054. S2CID 37962500. 
  15. ↑ A. Taflove; K. R. Umashankar (1983). 《Radar cross section of general three-dimensional scatterers》 (PDF). 《IEEE Trans. Electromagn. Compat.》 25. 433–440쪽. doi:10.1109/TEMC.1983.304133. S2CID 40419955. 
  16. ↑ 가 나 Z. P. Liao; H. L. Wong; B. P. Yang; Y. F. Yuan (1984). 《A transmitting boundary for transient wave analysis》. 《Scientia Sinica, Series A》 27. 1063–1076쪽. 
  17. ↑ W. Gwarek (1985). 《Analysis of an arbitrarily shaped planar circuit — A time-domain approach》. 《IEEE Transactions on Microwave Theory and Techniques》 33. 1067–1072쪽. Bibcode:1985ITMTT..33.1067G. doi:10.1109/TMTT.1985.1133170. 
  18. ↑ D. H. Choi; W. J. Hoefer (1986). 《The finite-difference time-domain method and its application to eigenvalue problems》. 《IEEE Transactions on Microwave Theory and Techniques》 34. 1464–1470쪽. Bibcode:1986ITMTT..34.1464C. doi:10.1109/TMTT.1986.1133564. 
  19. ↑ G. A. Kriegsmann; A. Taflove; K. R. Umashankar (1987). 《A new formulation of electromagnetic wave scattering using an on-surface radiation boundary condition approach》 (PDF). 《IEEE Transactions on Antennas and Propagation》 35. 153–161쪽. Bibcode:1987ITAP...35..153K. doi:10.1109/TAP.1987.1144062. 
  20. ↑ T. G. Moore; J. G. Blaschak; A. Taflove; G. A. Kriegsmann (1988). 《Theory and application of radiation boundary operators》 (PDF). 《IEEE Transactions on Antennas and Propagation》 36. 1797–1812쪽. Bibcode:1988ITAP...36.1797M. doi:10.1109/8.14402. 
  21. ↑ K. R. Umashankar; A. Taflove; B. Beker (1987). 《Calculation and experimental validation of induced currents on coupled wires in an arbitrary shaped cavity》 (PDF). 《IEEE Transactions on Antennas and Propagation》 35. 1248–1257쪽. Bibcode:1987ITAP...35.1248U. doi:10.1109/TAP.1987.1144000. 
  22. ↑ A. Taflove; K. R. Umashankar; B. Beker; F. A. Harfoush; K. S. Yee (1988). 《Detailed FDTD analysis of electromagnetic fields penetrating narrow slots and lapped joints in thick conducting screens》 (PDF). 《IEEE Transactions on Antennas and Propagation》 36. 247–257쪽. Bibcode:1988ITAP...36..247T. doi:10.1109/8.1102. 
  23. ↑ T. G. Jurgens; A. Taflove; K. R. Umashankar; T. G. Moore (1992). 《Finite-difference time-domain modeling of curved surfaces》 (PDF). 《IEEE Transactions on Antennas and Propagation》 40. 357–366쪽. Bibcode:1992ITAP...40..357J. doi:10.1109/8.138836. 
  24. ↑ D. M. Sullivan; O. P. Gandhi; A. Taflove (1988). 《Use of the finite-difference time-domain method in calculating EM absorption in man models》 (PDF). 《IEEE Transactions on Biomedical Engineering》 35. 179–186쪽. doi:10.1109/10.1360. PMID 3350546. S2CID 20350396. 
  25. ↑ X. Zhang; J. Fang; K. K. Mei; Y. Liu (1988). 《Calculation of the dispersive characteristics of microstrips by the time-domain finite-difference method》. 《IEEE Transactions on Microwave Theory and Techniques》 36. 263–267쪽. Bibcode:1988ITMTT..36..263Z. doi:10.1109/22.3514. 
  26. ↑ T. Kashiwa; I. Fukai (1990). 《A treatment by FDTD method of dispersive characteristics associated with electronic polarization》. 《Microwave and Optical Technology Letters》 3. 203–205쪽. doi:10.1002/mop.4650030606. 
  27. ↑ R. Luebbers; F. Hunsberger; K. Kunz; R. Standler; M. Schneider (1990). 《A frequency-dependent finite-difference time-domain formulation for dispersive materials》. 《IEEE Trans. Electromagn. Compat.》 32. 222–227쪽. doi:10.1109/15.57116. 
  28. ↑ R. M. Joseph; S. C. Hagness; A. Taflove (1991). 《Direct time integration of Maxwell's equations in linear dispersive media with absorption for scattering and propagation of femtosecond electromagnetic pulses》 (PDF). 《Optics Letters》 16. 1412–4쪽. Bibcode:1991OptL...16.1412J. doi:10.1364/OL.16.001412. PMID 19776986. 
  29. ↑ J. G. Maloney; G. S. Smith; W. R. Scott Jr. (1990). 《Accurate computation of the radiation from simple antennas using the finite-difference time-domain method》. 《IEEE Transactions on Antennas and Propagation》 38. 1059–1068쪽. Bibcode:1990ITAP...38.1059M. doi:10.1109/8.55618. S2CID 31583883. 
  30. ↑ D. S. Katz; A. Taflove; M. J. Piket-May; K. R. Umashankar (1991). 《FDTD analysis of electromagnetic wave radiation from systems containing horn antennas》 (PDF). 《IEEE Transactions on Antennas and Propagation》 39. 1203–1212쪽. Bibcode:1991ITAP...39.1203K. doi:10.1109/8.97356. 
  31. ↑ P. A. Tirkas; C. A. Balanis (1991). 〈Finite-difference time-domain technique for radiation by horn antennas〉. 《Antennas and Propagation Society Symposium 1991 Digest》 3. 1750–1753쪽. doi:10.1109/APS.1991.175196. ISBN 978-0-7803-0144-3. S2CID 122038624. 
  32. ↑ E. Sano; T. Shibata (1990). 《Fullwave analysis of picosecond photoconductive switches》. 《IEEE Journal of Quantum Electronics》 26. 372–377쪽. Bibcode:1990IJQE...26..372S. doi:10.1109/3.44970. 
  33. ↑ S. M. El-Ghazaly; R. P. Joshi; R. O. Grondin (1990). 《Electromagnetic and transport considerations in subpicosecond photoconductive switch modeling》. 《IEEE Transactions on Microwave Theory and Techniques》 38. 629–637쪽. Bibcode:1990ITMTT..38..629E. doi:10.1109/22.54932. 
  34. ↑ P. M. Goorjian; A. Taflove (1992). 《Direct time integration of Maxwell's equations in nonlinear dispersive media for propagation and scattering of femtosecond electromagnetic solitons》 (PDF). 《Optics Letters》 17. 180–182쪽. Bibcode:1992OptL...17..180G. doi:10.1364/OL.17.000180. PMID 19784268. 
  35. ↑ R. W. Ziolkowski; J. B. Judkins (1993). 《Full-wave vector Maxwell's equations modeling of self-focusing of ultra-short optical pulses in a nonlinear Kerr medium exhibiting a finite response time》. 《Journal of the Optical Society of America B》 10. 186–198쪽. Bibcode:1993JOSAB..10..186Z. doi:10.1364/JOSAB.10.000186. 
  36. ↑ R. M. Joseph; P. M. Goorjian; A. Taflove (1993). 《Direct time integration of Maxwell's equations in 2-D dielectric waveguides for propagation and scattering of femtosecond electromagnetic solitons》 (PDF). 《Optics Letters》 18. 491–3쪽. Bibcode:1993OptL...18..491J. doi:10.1364/OL.18.000491. PMID 19802177. 
  37. ↑ R. M. Joseph; A. Taflove (1994). 《Spatial soliton deflection mechanism indicated by FDTD Maxwell's equations modeling》 (PDF). 《IEEE Photonics Technology Letters》 2. 1251–1254쪽. Bibcode:1994IPTL....6.1251J. doi:10.1109/68.329654. S2CID 46710331. 
  38. ↑ W. Sui; D. A. Christensen; C. H. Durney (1992). 《Extending the two-dimensional FDTD method to hybrid electromagnetic systems with active and passive lumped elements》. 《IEEE Transactions on Microwave Theory and Techniques》 40. 724–730쪽. Bibcode:1992ITMTT..40..724S. doi:10.1109/22.127522. 
  39. ↑ B. Toland; B. Houshmand; T. Itoh (1993). 《Modeling of nonlinear active regions with the FDTD method》. 《IEEE Microwave and Guided Wave Letters》 3. 333–335쪽. doi:10.1109/75.244870. S2CID 27549555. 
  40. ↑ Aoyagi, P.H.; Lee, J.F.; Mittra, R. (1993). 《A hybrid Yee algorithm/scalar-wave equation approach》. 《IEEE Transactions on Microwave Theory and Techniques》 41. 1593–1600쪽. Bibcode:1993ITMTT..41.1593A. doi:10.1109/22.245683. 
  41. ↑ V. A. Thomas; M. E. Jones; M. J. Piket-May; A. Taflove; E. Harrigan (1994). 《The use of SPICE lumped circuits as sub-grid models for FDTD high-speed electronic circuit design》 (PDF). 《IEEE Microwave and Guided Wave Letters》 4. 141–143쪽. doi:10.1109/75.289516. S2CID 32905331. 
  42. ↑ 가 나 다 라 J. Berenger (1994). 《A perfectly matched layer for the absorption of electromagnetic waves》 (PDF). 《Journal of Computational Physics》 114. 185–200쪽. Bibcode:1994JCoPh.114..185B. doi:10.1006/jcph.1994.1159. 
  43. ↑ 가 나 E.A. Navarro; C. Wu; P.Y. Chung; J. Litva (1994). 《Application of PML superabsorbing boundary condition to non-orthogonal FDTD method》. 《Electronics Letters》 30. 1654–1656쪽. Bibcode:1994ElL....30.1654N. doi:10.1049/el:19941139. 
  44. ↑ D. S. Katz; E. T. Thiele; A. Taflove (1994). 《Validation and extension to three dimensions of the Berenger PML absorbing boundary condition for FDTD meshes》 (PDF). 《IEEE Microwave and Guided Wave Letters》 4. 268–270쪽. doi:10.1109/75.311494. S2CID 10156811. 
  45. ↑ C. E. Reuter; R. M. Joseph; E. T. Thiele; D. S. Katz; A. Taflove (1994). 《Ultrawideband absorbing boundary condition for termination of waveguiding structures in FDTD simulations》 (PDF). 《IEEE Microwave and Guided Wave Letters》 4. 344–346쪽. doi:10.1109/75.324711. S2CID 24572883. 
  46. ↑ W.C. Chew; W.H. Weedon (1994). 《A 3D perfectly matched medium from modified Maxwell's equations with stretched coordinates》. 《Microwave and Optical Technology Letters》 7. 599–604쪽. Bibcode:1994MiOTL...7..599C. doi:10.1002/mop.4650071304. 
  47. ↑ 가 나 다 S. D. Gedney (1996). 《An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices》. 《IEEE Transactions on Antennas and Propagation》 44. 1630–1639쪽. Bibcode:1996ITAP...44.1630G. doi:10.1109/8.546249. 
  48. ↑ Z. S. Sacks; D. M. Kingsland; R. Lee; J. F. Lee (1995). 《A perfectly matched anisotropic absorber for use as an absorbing boundary condition》. 《IEEE Transactions on Antennas and Propagation》 43. 1460–1463쪽. Bibcode:1995ITAP...43.1460S. doi:10.1109/8.477075. 
  49. ↑ Q. H. Liu (1997). 〈The pseudospectral time-domain (PSTD) method: A new algorithm for solutions of Maxwell's equations〉. 《IEEE Antennas and Propagation Society International Symposium 1997. Digest》 1. 122–125쪽. doi:10.1109/APS.1997.630102. ISBN 978-0-7803-4178-4. S2CID 21345353. 
  50. ↑ O. M. Ramahi (1997). 《The complementary operators method in FDTD simulations》. 《IEEE Antennas and Propagation Magazine》 39. 33–45쪽. Bibcode:1997IAPM...39...33R. doi:10.1109/74.646801. 
  51. ↑ J. G. Maloney; M. P. Kesler (1998). 《Analysis of Periodic Structures》. 《Chap. 6 in Advances in Computational Electrodynamics: The Finite-Difference Time-Domain Method, A. Taflove, Ed., Artech House, Publishers》. 
  52. ↑ A. S. Nagra; R. A. York (1998). 《FDTD analysis of wave propagation in nonlinear absorbing and gain media》. 《IEEE Transactions on Antennas and Propagation》 46. 334–340쪽. Bibcode:1998ITAP...46..334N. doi:10.1109/8.662652. 
  53. ↑ S. C. Hagness; A. Taflove; J. E. Bridges (1998). 《Two-dimensional FDTD analysis of a pulsed microwave confocal system for breast cancer detection: Fixed-focus and antenna-array sensors》 (PDF). 《IEEE Transactions on Biomedical Engineering》 45. 1470–1479쪽. doi:10.1109/10.730440. PMID 9835195. S2CID 6169784. 
  54. ↑ J. B. Schneider; C. L. Wagner (1999). 《FDTD dispersion revisited: Faster-than-light propagation》. 《IEEE Microwave and Guided Wave Letters》 9. 54–56쪽. CiteSeerX 10.1.1.77.9132. doi:10.1109/75.755044. 
  55. ↑ F. Zhen; Z. Chen; J. Zhang (2000). 《Toward the development of a three-dimensional unconditionally stable finite-difference time-domain method》. 《IEEE Transactions on Microwave Theory and Techniques》 48. 1550–1558쪽. Bibcode:2000ITMTT..48.1550Z. doi:10.1109/22.869007. 
  56. ↑ F. Zheng; Z. Chen (2001). 《Numerical dispersion analysis of the unconditionally stable 3-D ADI-FDTD method》. 《IEEE Transactions on Microwave Theory and Techniques》 49. 1006–1009쪽. Bibcode:2001ITMTT..49.1006Z. doi:10.1109/22.920165. 
  57. ↑ J. A. Roden; S. D. Gedney (2000). 《Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media》. 《Microwave and Optical Technology Letters》 27. 334–339쪽. doi:10.1002/1098-2760(20001205)27:5<334::AID-MOP14>3.0.CO;2-A. 2013년 1월 5일에 원본 문서에서 보존된 문서. 
  58. ↑ T. Rylander; A. Bondeson (2000). 《Stable FDTD-FEM hybrid method for Maxwell's equations》. 《Computer Physics Communications》 125. 75–82쪽. doi:10.1016/S0010-4655(99)00463-4. 
  59. ↑ M. Hayakawa; T. Otsuyama (2002). 《FDTD analysis of ELF wave propagation in inhomogeneous subionospheric waveguide models》. 《ACES Journal》 17. 239–244쪽. 2012년 5월 27일에 원본 문서에서 보존된 문서. 
  60. ↑ J. J. Simpson; A. Taflove (2002). 《Two-dimensional FDTD model of antipodal ELF propagation and Schumann resonance of the Earth》 (PDF). 《IEEE Antennas and Wireless Propagation Letters》 1. 53–56쪽. Bibcode:2002IAWPL...1...53S. CiteSeerX 10.1.1.694.4837. doi:10.1109/LAWP.2002.805123. S2CID 368964. 2010년 6월 17일에 원본 문서 (PDF)에서 보존된 문서. 
  61. ↑ H. De Raedt; K. Michielsen; J. S. Kole; M. T. Figge (2003). 《Solving the Maxwell equations by the Chebyshev method: A one-step finite difference time-domain algorithm》. 《IEEE Transactions on Antennas and Propagation》 51. 3155–3160쪽. arXiv:physics/0208060. Bibcode:2003ITAP...51.3155D. doi:10.1109/TAP.2003.818809. S2CID 119095479. 
  62. ↑ A. Soriano; E.A. Navarro; J. Portí; V. Such (2004). 《Analysis of the finite difference time domain technique to solve the Schrödinger equation for quantum devices》. 《Journal of Applied Physics》 95. 8011–8018쪽. Bibcode:2004JAP....95.8011S. doi:10.1063/1.1753661. hdl:10550/12837. 
  63. ↑ I. Ahmed; E. K. Chua; E. P. Li; Z. Chen (2008). 《Development of the three-dimensional unconditionally stable LOD-FDTD method》. 《IEEE Transactions on Antennas and Propagation》 56. 3596–3600쪽. Bibcode:2008ITAP...56.3596A. doi:10.1109/TAP.2008.2005544. S2CID 31351974. 
  64. ↑ Taniguchi, Y.; Baba, Y.; N. Nagaoka; A. Ametani (2008). 《An Improved Thin Wire Representation for FDTD Computations》. 《IEEE Transactions on Antennas and Propagation》 56. 3248–3252쪽. Bibcode:2008ITAP...56.3248T. doi:10.1109/TAP.2008.929447. S2CID 29617214. 
  65. ↑ R. M. S. de Oliveira; C. L. S. S. Sobrinho (2009). 《Computational Environment for Simulating Lightning Strokes in a Power Substation by Finite-Difference Time-Domain Method》. 《IEEE Transactions on Electromagnetic Compatibility》 51. 995–1000쪽. doi:10.1109/TEMC.2009.2028879. 
  66. ↑ R. M. S. de Oliveira; R. R. Paiva (2021). 《Least Squares Finite-Difference Time-Domain》. 《IEEE Transactions on Antennas and Propagation》 69. 6111–6115쪽. Bibcode:2021ITAP...69.6111D. doi:10.1109/TAP.2021.3069576. S2CID 234307029. 
  67. ↑ “Fitting of dielectric function”. 
  68. ↑ I. Valuev; A. Deinega; S. Belousov (2008). 《Iterative technique for analysis of periodic structures at oblique incidence in the finite-difference time-domain method》. 《Opt. Lett.》 33. 1491–3쪽. Bibcode:2008OptL...33.1491V. doi:10.1364/ol.33.001491. PMID 18594675. 
  69. ↑ A. Aminian; Y. Rahmat-Samii (2006). 《Spectral FDTD: a novel technique for the analysis of oblique incident plane wave on periodic structures》. 《IEEE Transactions on Antennas and Propagation》 54. 1818–1825쪽. Bibcode:2006ITAP...54.1818A. doi:10.1109/tap.2006.875484. S2CID 25120679. 
  70. ↑ A. Deinega; S. Belousov; I. Valuev (2009). 《Hybrid transfer-matrix FDTD method for layered periodic structures》. 《Opt. Lett.》 34. 860–2쪽. Bibcode:2009OptL...34..860D. doi:10.1364/ol.34.000860. PMID 19282957. S2CID 27742034. 
  71. ↑ Y. Hao; R. Mittra (2009). 《FDTD Modeling of Metamaterials: Theory and Applications》. Artech House Publishers. 
  72. ↑ D. Gallagher (2008). 《Photonics CAD Matures》 (PDF). 《LEOS Newsletter》. 
  73. ↑ A. Deinega; I. Valuev (2011). 《Long-time behavior of PML absorbing boundaries for layered periodic structures》. 《Comput. Phys. Commun.》 182. 149–151쪽. Bibcode:2011CoPhC.182..149D. doi:10.1016/j.cpc.2010.06.006. 
  74. ↑ S. G. Johnson, "Numerical methods for computing Casimir interactions," in Casimir Physics (D. Dalvit, P. Milonni, D. Roberts, and F. da Rosa, eds.), vol. 834 of Lecture Notes in Physics, ch. 6, pp. 175–218, Berlin: Springer, June 2011.

더 읽어보기

[편집]

Nature Milestones: Photons의 다음 기사는 맥스웰 방정식과 관련된 FDTD 방법의 역사적 중요성을 보여준다:

앨런 태플로브의 인터뷰, "Numerical Solution", 2015년 1월 네이처 포토닉스 특집호에 실린 맥스웰 방정식 출판 150주년 기념. 이 인터뷰는 FDTD 개발이 맥스웰 전자기학 이론의 150년 역사와 어떻게 연결되는지 다루고 있다:

다음 대학 수준 교과서들은 FDTD 방법에 대한 좋은 일반적인 소개를 제공한다:

외부 링크

[편집]
위키미디어 공용에 FDTD법 주제와 관련된 미디어 분류가 있습니다.

자유 소프트웨어/오픈 소스 소프트웨어 FDTD 프로젝트:

프리웨어/클로즈드 소스 FDTD 프로젝트 (일부는 상업적 용도로 사용할 수 없음):

원본 주소 "https://ko.wikipedia.org/w/index.php?title=FDTD법&oldid=40822446"