乘法

3×4 = 12

乘法是四则运算之一。乘法运算的本质，就是​​“同类累加的简写形式​​”。

例如：

$a\times b=\underbrace {b+\cdots +b} _{a{\text{ 个 b}}}.$

$a$ 和 $b$ 都是本式的因数（或称约数），其運算結果稱為積。

$a\times b$可以唸作「a 乘 b」（“a times b”）或「a 乘以 b」（“a multiplied by b”）。唸作「a 乘 b」时 $a$ 是乘数，$b$ 是被乘数，即“$a$个$b$”。唸作「a 乘以 b」则相反，表示“$a$的$b$倍”。这种双意并非中文或者英文特有。乘数和被乘数的交替并不会影响乘法的结果。

乘法运算亦有其它形象理解：对于整数乘法，可表现为将对象排列成矩形陣列；对于实数乘法，则可解释为计算矩形面积。同样地，运算结果不受边长测量顺序的影响。

在乘法基本概念的基础上，序列乘积、向量乘法、复数及矩阵运算等均对其进行了概念扩展。这些更高级的数学结构会以各自方式影响乘法的基本性质——例如矩阵乘法和某些向量乘法会呈现非交换性，复数乘法则会改变复数的符号。

引言

首先，进入正题前，我们不妨来看两个生活中的例子：

• 买5个单价为3圆的冰激凌：由$5\times 3=15$可得，需要支付15圆。
• 要搭一个3层高、每层4块积木的小塔：由$3\times 4=12$可得，需要12块积木。

其次，数学和物理存在许多“累加关系”：

• 已知匀速直线运动状态下，某物体行进速度为 $v$ ，所用时间为 $t$ ，可得累计距离 $d=v\times t$ ；
• 已知一个物体的密度为 $\rho$ （假设密度均匀），体积为 $V$ ，可得其质量 $m=\rho \times V$ ；

......

可见，在数学，尤其是在基本算术中，乘法是​​加法的“快捷版”​​。

定义

基本定义

乘法运算，指通过特定法则将两个或多个数结合生成积的运算过程。其核心内涵包括：

1. 同类累加的简写形式：表示将相同值的数进行连续叠加的运算（如 $3\times 4=4+4+4=12$ ）
2. 比例关系的量化表达：当乘数非整数时，可表示为原数的分数（小数）倍（如 $3\times 0.5$ 表示 $3$ 的一半，$4\times {\dfrac {1}{3}}$ 表示 $4$ 的三分之一）
3. 維度扩展的数学工具：在几何学中，用于计算面积（长 $\times$ 宽）、体积（长 $\times$ 宽 $\times$ 高）等空间度量

符号与表示

主条目：乘号

乘法可以用幾種方法表示。以下的式子表示“五乘以二”：

• $5\times 2$
• $5\cdot 2$
• $5*2$
• $(5)(2)$

古代常用的方法是將兩個數並排，沒有甚麼特別的符號來表示乘法。

以「$\times$」表示乘法，是由奥特雷德于1618年最先引入，也是現在最流行的寫法。在计算机领域，也有為方便鍵盤輸入而以小寫英文字母「x」替代「×」。

以「$\cdot$」表示乘法，如今已成为美国、德國、法國等國家的标准。其最早由托马斯·哈里奥特于1631年出版的著作使用，但令這种用法影响深远的人是萊布尼茲。

因為星號「$*$」是鍵盤必備的符號，電腦常用其表示乘號，这种用法起源于FORTRAN语言。

代数中，为方便书写，乘號常被略去（如 $5x$ 和 $xy$ ）。但如果變數多於一個字母，则易令人混淆。同时如果只有數字，乘号则不应略去，如 $5\times 2$ 不會表示成 $52$ 。

累乘则用大写希臘字母 $\Pi$（Pi）表示：

$\prod _{i=m}^{n}x_{i}:=x_{m}\cdot x_{m+1}\cdot x_{m+2}\cdot \ldots \cdot x_{n-1}\cdot x_{n}$

性质

乘法运算的数学性质在不同定义和數系下具有多样性，以下是主要分类及详细说明。

基本运算律

1. 交換律：$xy=yx$
2. 結合律：$(xy)z=x(yz)$
3. 分配律：$x(y+z)=xy+xz$

单位元、零元与逆元性质

1. 乘法單位律：任何数乘以 $1$ ，都會等於該數本身，即$1x=x$。此律可扩展至多項式中的常数项。
2. 零元性质：任何數乘以 $0$ ，即是甚麼也沒做過，結果为零，即$0x=0$。同样地，多个因數中若含 $0$ ，积必为 $0$ 。
3. 逆元性质：非零数 $a$ 的逆元（亦为其倒数）为 ${\dfrac {1}{a}}$ ，满足 $a\times {\dfrac {1}{a}}=1$ 。

特殊数系下的性质

实数与复数除法

1. 满足交换律、结合律、分配律。
2. 复数乘法涉及模长和辐角的变化。

矩阵乘法

1. 满足结合律和分配律，但​​不满足交换律，特殊矩阵（如對角矩陣）除外。
2. 对零矩陣：所有元素为 $0$ 的矩阵，与任意矩阵相乘结果为零矩阵。

模运算

在模 $n$ 下，乘法逆元存在当且仅当数与 $n$ 互質（如模质数时所有非零数均有逆元）。

不同的乘法运算

两个数的乘法运算或积（这两个数可以是自然数、整数、分数、实数、复数、四元数等）的数学定义，相似而又各有特性。

自然数乘法

兩個自然數 $m,n\in \mathbb {N}$ ，其乘積为：

$mn=nm=\sum _{k=1}^{n}m=\sum _{k=1}^{m}n$

這是将该整数自身重复相加若干次的簡写法。换言之：

$mn=nm=\underbrace {m+m+m+\cdots +m} _{n{\text{个 m}}}=\underbrace {n+n+n+\cdots +n} _{m{\text{个 n}}}$

长远来看，将乘法视为重复加法并不高效。因此，数学家归纳了从 $1$ 到 $9$ 的乘法结果，即九九乘法表。

多个自然数相乘时，我们使用括号标明运算顺序。为避免过多括号，规定以下优先级规则：乘法始终优先于加法。例如在表达式 $4+5\times 2$ 中，应理解为 $4+(5\times 2)=4+10=14$ ，而非 $(4+5)\times 2=9\times 2=18$ 。

當$x$是量，$y$是自然數时，定義乘法递归如下：

$0x=0$

$xy=x+x(y-1)$

整数乘法

图中，笛卡儿坐标系的蓝色区域表示乘积为正，红色区域表示乘积为负。

在数轴上表示整数乘法时，可借助向量的方向与长度直观理解

整数乘法推广自然数乘法至负数，符号规则为：同号得正，异号得负，绝对值相乘。

分数（小数）乘法

两个分數 ${\frac {z}{n}},{\frac {z'}{n'}}$ 作乘法运算时，分子与分子相乘，分母与分母相乘：

${\frac {z}{n}}\cdot {\frac {z'}{n'}}={\frac {z\cdot z'}{n\cdot n'}}$

当且仅当 $n,n'\neq 0$ 时成立。

两个小数作乘法运算时，可利用乘法交换律的特性进行计算。

例如，计算 $43.1$ 乘以 $1.215$ 时：

${\begin{aligned}43.1\times 1.215&=\left(431\times {\frac {1}{10}}\right)\times \left(1\;215\times {\frac {1}{1\;000}}\right)\\&=(431\times 1\;215)\times \left({\frac {1}{10}}\times {\frac {1}{1\;000}}\right)\\&=(431\times 1\;215)\times {\frac {1}{10\;000}}\\&={\frac {523\;665}{10\;000}}\\&=52.3665\end{aligned}}$

可见，两个小数作乘法运算时，先忽略小數點，计算两数小数点后数字的位数之和，将两数视为整数相乘，最后在结果中从右往左数出与总位数相同的位数，并放置小数点。

又如，计算 $3.15$ 乘以 $1.2$ 时：

1. 先计算整数部分相乘：$315\times 12=3780$
2. 再将小数点向左移动 $3$ 位：$3780\Rightarrow 3.780$（末尾的 $0$ 可省略，写作 $3.78$）

实数乘法

实数乘法是前文乘法的推广，性质也相同。其核心在于：每个实数都是某有理数集的上确界。特别地，每个正实数是其无限小数展开式截断序列的上确界，例如 $\pi$ 是集合 $\{3,\;3.1,\;3.14,\;3.141,\ldots \}$ 的上确界。

实数的一个基本性质是：有理逼近与算术运算（特别是乘法）相容。这意味着，若正实数 $a$ 和 $b$ 分别表示为集合 $A$ 和 $B$ 的上确界（即 $a=\sup _{x\in A}x$ ， $b=\sup _{y\in B}y$ ），则两数乘积 $a\cdot b$ 等于所有 $x\in A$ 与 $y\in B$ 的乘积项的上确界（即 $a\cdot b=\sup _{x\in A,y\in B}x\cdot y$ ）。具体而言，两个正实数的乘积等于其十进制展开式逐项积序列的上确界。

对于涉及负实数的乘法运算，可通过符号法则简化处理：正负号的变化将上确界转化为下确界。很多人都通过柯西序列构造实数，因为这种方法无需考虑四种可能的符号组合情况，从而简化了运算规则的推导过程。

复数乘法

复数乘法可通过分配律和虚数单位性质 $i^{2}=-1$ 进行运算。具体地，两个复数 $(a+b\,i)$ 与 $(c+d\,i)$ 作乘法运算时，展开过程为：

${\begin{aligned}(a+b\,i)\cdot (c+d\,i)&=a\cdot c+a\cdot d\,i+b\,i\cdot c+b\cdot d\cdot i^{2}\\&=(a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)\,i\end{aligned}}$

其中 $i^{2}$ 替换为 $-1$ 后，实部与虚部分别合并。

用极坐标系表示复数

从几何视角理解，复数可表示为极坐标形式：

$a+b\,i=r\cdot (\cos(\varphi )+i\sin(\varphi ))=r\cdot e^{i\varphi }$

$c+d\,i=s\cdot (\cos(\psi )+i\sin(\psi ))=s\cdot e^{i\psi }$

此时，复数乘法可转化为模长与辐角的运算：

$(a\cdot c-b\cdot d)+(a\cdot d+b\cdot c)i=r\cdot s\cdot e^{i(\varphi +\psi )}.$

其几何意义在于模长相乘（ $r\cdot s$ ）、辐角相加（ $\varphi +\psi$ ）。

四元数乘法

参见：四元数 § 加、乘和一般函數

基于集合论的乘法

非负整数的乘法可通过集合论中的基数概念或皮亚诺公理进行定义。基数理论通过集合的势（即集合元素的数量）定义乘法，例如，两个有限集合的笛卡儿积的势等于各自势的乘积。而皮亚诺公理体系则通过自然数的递归定义实现乘法运算：设非负整数表示为自然数，其乘法可归纳定义为：

• 基例​​：对任意非负整数 $a$ ，有 $a\times 0=0$ ；
• 递推规则​​：对任意非负整数 $a$ 、$b$ ，有 $a\times {(b+1)}=a\times b+a$ 。

此定义通过数学归纳法可证明满足乘法结合律、交换律等基本性质。

对于任意整数的乘法，需在自然数乘法基础上引入符号规则。例如，负整数乘法定义为：若 $a$ 、$b$ 为自然数，则 ${(-a)}\times {(-b)}=a\times b$ ，而 ${(-a)}\times b=-{(a\times b)}$ 。这一扩展保持了乘法运算的代数结构一致性。

有理数乘法则通过分数形式定义：若 ${\dfrac {a}{b}}$ 与 ${\dfrac {c}{d}}$ 为最简分数（ $b$ 、$d\neq 0$ ），则其乘积为 ${\dfrac {ac}{bd}}$ ，分母通过集合论中的笛卡尔积构造，分子通过自然数乘法定义。此过程需验证运算的封闭性与唯一性，例如通过交叉相乘消去公约数，确保结果仍为最简分数。

实数乘法的定义依赖于有理数乘法的完备性。通过戴德金分割或柯西序列构造实数时，乘法运算被定义为极限运算：若 $\{a_{n}\}$ 和 $\{b_{n}\}$ 为收敛的有理数序列，则实数乘积定义为 $\lim(a_{n}\times b_{n})$ 。此定义需满足乘法与极限运算的交换性，并通过 $\epsilon -\delta$ 语言严格证明其合理性。

基于群论的乘法

在群论中，若一个集合在乘法运算下满足封闭性、结合律、存在单位元且每个元素均有逆元素，则称其构成群结构。这些公理构成了群的定义基础。

以非零有理数集为例，其乘法运算满足群的所有条件：单位元为1（不同于加法群的单位元0），每个非零有理数均存在乘法逆元，且乘法运算封闭（因为两个非零有理数相乘仍为非零有理数）。但需注意的是，零必须被排除，因其乘法逆元不存在。此例中的群为阿贝尔群，但群论中并非所有乘法群均为阿贝尔群。

考虑可逆方阵群：给定域上同维数的可逆矩阵集合，其乘法运算满足封闭性（矩阵相乘仍为同维可逆矩阵）、结合律、单位矩阵作为单位元，且每个矩阵均有逆矩阵。然而，矩阵乘法不满足交换律（如 ${AB}\neq {BA}$ ），因此该群为非阿贝尔群。

即使排除零元素，整数集在乘法下也不构成群。原因在于除 $1$ 和 $-1$ 外，其他整数均无乘法逆元。这一特性凸显了乘法群对逆元存在与否的严格要求。

群的乘号通常表示为点乘（$\cdot$）或直接省略不写。在描述群时，点乘符号常用于明确运算，例如非零有理数乘法群可记为（ $\mathbb {Q} \{0\},\cdot$ ）。这种符号体系与加法群（如（ $\mathbb {Z} ,+$ ））形成对比，体现了运算类型的差异。

运算方法

历史上的算法

迄今为止发现的最早的乘法运算，是可追溯至旧石器时代初期的伊尚戈骨上的刻痕。划痕可能是计数符号，也可能只是为了方便抓握，或有其他非数学的目的。

古埃及人采用连续加倍法进行整数和分數的乘法运算，这一方法在《莱因德数学纸草书》中有详细记载。例如，计算 $13\times 21$ 时，通过将$21$依次加倍三次得到$42$、$84$、$168$，再根据加倍序列中的对应项，得出 ${(1+4+8)}\times 21=273$ 。

巴比伦人使用六十進制系统，其乘法运算与现代十进制类似，但因 $60\times 60=3600$ 种组合过多，他们通过制作包含前$20$个基数倍數的乘法表（如 $n,2n,\ldots ,20n$ 及 $30n,40n,50n$ ）来简化计算，如 $53n$ 可通过 $50n+3n$ 的组合快速得出。

古希腊人以幾何圖形（如矩形）表示乘法，体现“乘积即面积”的思想。欧几里得更是在《几何原本》中用几何方法证明乘法分配律。

孙子筹算乘法

中国古代拥有史上最早、最详细的​​十进制位值制乘法规则，其首见于南北朝时期的孙子算经。孙子乘法的核心，是通过纵横排列的算筹模拟位值运算，如计算 $49\times 36$ 时，先以算筹摆出 $49$ 和 $36$ ，再按“九九表”逐位相乘并累加，终得 $1764$ 。这种算法在9世纪传至中东，13世纪又译成拉丁文而流行于欧洲。至于九九乘法表​​，则在战国时期已成熟应用，其采用“小九九”形式，从“九九八十一”到“一一如一”，比古埃及的累加法效率提升数十倍。

阿拉伯穆斯林于9世纪引入印度數字和位值制，结合阿拉伯语符号形成计算体系，推动乘法运算标准化。而数学家花拉子米在接纳中国的孙子乘法後，在《代数学》中将乘法与方程系统化结合，提出“还原与对消”法，将乘法纳入代数运算框架，影响欧洲数学发展。

印度类似“铺地锦”的图形化乘法

納皮爾的骨頭

印度古代的乘法运算亦有发展。7世纪，数学家婆羅摩笈多提出“交叉相乘法”，即 $(a+b)(c+d)=ac+ad+bc+bd$ ，简化多位数乘法步骤。例如计算 ${123}\times {456}$ 时，通过分项相乘再求和，减少重复计算。12世纪，印度文献中出现类似中国古代“铺地锦”的图形化乘法，通过网格线段交叉点计数得出结果，后经阿拉伯传入欧洲。“納皮爾的骨頭”便是借鉴“铺地锦”的灵感产生的。

现代算法

现代基于印度-阿拉伯数字系统的乘法，最早同样由婆罗摩笈多系统阐述。他在7世纪著作《婆罗摩修正体系》中完整定义了加、减、乘、除四则运算的规则，其乘法体系包含多种算法，现代竖式乘法即源于此。此算法通过花拉子米的著作《印度数字算术》于9世纪初传入阿拉伯世界，其《代数学》系统整合了印度数字与运算规则。13世纪，意大利数学家斐波那契在《计算之书》中推广此法，最终使印度-阿拉伯数字系统取代罗马数字成为欧洲主流。

由于历史影响，華人小學生现在仍背誦九九乘法表來學習乘法。

关于電腦的特別算法，以及其它现代运算法，详見乘法算法。

其它算法

用手指算乘法

除了加法，在有限范围内，乘法也可以用手指完成。为此，两个因數需处于同一十位半区，也就是说，两者要么均以 $1$ 至 $5$ 结尾，要么均以 $6$ 至 $0$ 结尾。

对于因数以 $1$ 至 $5$ 结尾的情况：

1. 首先为手指编号：从小指开始，依次标记为 $10\cdot {(d-1)}+1$ 至拇指为 $10\cdot {(d-1)}+5$ （其中 $d$ 表示对应数的十位，如第二位为 $1$ 时，对应 $11$ 至 $15$ ）；
2. 对齐两个因数的手指後，数出下方手指总数（包括对齐的手指），将其乘以 $d\cdot 10$ ；
3. 计算左右手下方手指（不包含对齐的手指）的乘积；
4. 最后，加上常数项 ${d^{2}}\cdot 100$ ，结果即为所求。

对于因数以 $6$ 至 $0$ 结尾的情况：

1. 类似地，从小指开始，依次标记为 $10\cdot {(d-1)}+6$ 至拇指为 $10\cdot d$ （其中 $d$ 表示对应数的十位，如第二位为 $1$ 时，对应 $16$ 至 $20$ ）；
2. 对齐两个因数的手指后，数出下方手指总数（包括对齐的手指），将其乘以 $d\cdot 10$ （同上）；
3. 计算左右手上方手指（不包含对齐的手指）的乘积（同上）；
4. 最后，加上常数项 $d\cdot {(d-1)}\cdot 100$ ，结果即为所求。

以 $7\times 8$ 为例： $7$ 和 $8$ 均以 $6$ 至 $0$ 结尾，而 $d=1$ 。对齐手指后，下方手指有 $5$ 根，乘以 $1\times 10=10$ 得 $50$ ；上方手指分别为 $3$ 根和 $2$ 根，积为 $3\times 2=6$ ；加法常数项 ${(1-1)}\cdot 1\cdot 100=0$，总和为 $50+6+0=56$ 。

再如 $24\times 22$ ： $24$ 和 $22$ 均以 $1$ 至 $5$ 结尾，而 $d=2$ 。对齐手指后，下方手指有 $6$ 根，乘以 $2\times 10=20$ 得到 $120$ ；下方手指分别为 $4$ 根和 $2$ 根，积为 $4\times 2=8$ ；加法常数项 ${2^{2}}\cdot 100=400$ ，总和为 $120+8+400=528$ 。

此方法尤其适用于快速心算平方数。对于不同十位或十位半区的因数，可通过分解为和的形式（如 ${(a+x)}\cdot {(a+y)}$ ）应用该技巧。其数学原理基于多项式展开：

$(a+x)\cdot (a+y)=a^{2}+(x+y)\cdot a+x\cdot y$

尺规作图法

从相交弦定理出发的尺规法

图1
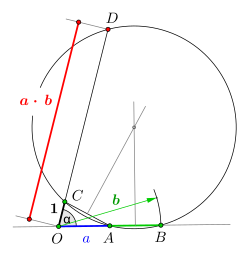
利用相交弦定理算乘法

如图1所示，过点 $O$ 作一直线，分别在 $O$ 点两侧截取长度为 $a$ 和 $b$ 的线段，得点 $A$ 和 $B$ 。再从 $O$ 出发，沿另一方向作射线，截取单位长度 $1$ ，得点 $E$ 。过 $A$ 、$B$ 、$E$ 三点作外接圓，该圆与第二条射线的交点 $C$ 满足相交弦定理：

$a\cdot b={\overline {OA}}\cdot {\overline {OB}}=\underbrace {\overline {OE}} _{=1}\cdot \,{\overline {OC}}$

${\overline {OE}}=1\Longrightarrow {\overline {OC}}=a\cdot b$

此法通过构造三角形外接圆，将乘法转化为几何长度的投影关系。

从割线定理出发的尺规法

图2
利用割线定理算乘法

如图2所示，设圆外一点 $O$ ，沿同一方向截取长度为 $a$ 和 $b$ 的线段，得点 $A$ 和 $B$ 。过 $O$ 作与 $BO$ 成任意角 $\alpha$ 的射线，在该射线上截取单位长度 $1$ ，得点 $C$ 。作 $AB$ 和 $AC$ 的垂直平分線以确定圆心，过 $A$ 、 $B$ 、 $C$ 三点作外接圆，该圆与射线交于点 $D$ 。根据割线定理：

$a\cdot b={\overline {OA}}\cdot {\overline {OB}}={\overline {OC}}\cdot \,{\overline {OD}}$

通过调整射线角度 $\alpha$ ，可利用相似三角形关系将乘积转化为圆外一点到交点的距离。

从相似三角形出发的尺规法

图3
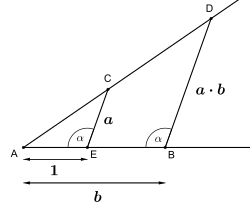
利用相似三角形算乘法

如图3所示，在射线 $A$ 上截取单位长度 $1$ 和长度 $b$ ，得点 $E$ 和 $B$ ，从 $E$ 出发，沿另一方向截取长度 $a$ ，得点 $C$ 。过 $C$ 作与 $AB$ 平行的直线，与过 $A$ 的射线交于点 $D$ 。由相似三角形关系可得：

${\dfrac {\overline {AB}}{\overline {AC}}}={\dfrac {\overline {BD}}{\overline {BC}}}\Longrightarrow {\overline {BD}}=a\cdot b$

此法通过构造平行线与相似三角形，将乘法运算转化为几何比例问题。