Phase velocity

Frequency dispersion in groups of gravity waves on the surface of deep water. The ■ red square moves with the phase velocity, and the ● green circles propagate with the group velocity. In this deep-water case, the phase velocity is twice the group velocity. The red square overtakes two green circles when moving from the left to the right of the figure.

New waves seem to emerge at the back of a wave group, grow in amplitude until they are at the center of the group, and vanish at the wave group front.

For surface gravity waves, the water particle velocities are much smaller than the phase velocity, in most cases.

Propagation of a wave packet demonstrating a phase velocity greater than the group velocity.

This shows a wave with the group velocity and phase velocity going in different directions. The group velocity is positive (i.e., the envelope of the wave moves rightward), while the phase velocity is negative (i.e., the peaks and troughs move leftward).

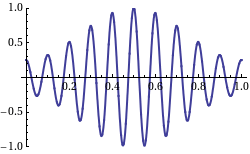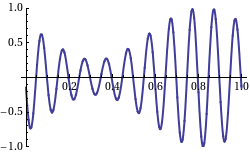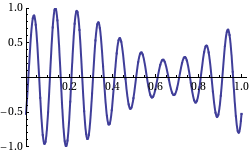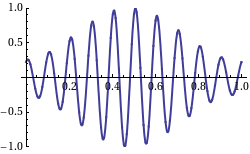
The phase velocity of a wave is the speed of any surface of constant phase. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity of light waves is not a physically meaningful quantity and is not related to information transfer.

Sinusoidal or plane waves

For a simple sinusoidal wave the phase velocity is given in terms of the wavelength λ (lambda) and time period T as

$v_{\mathrm {p} }={\frac {\lambda }{T}}.$

Equivalently, in terms of the wave's angular frequency ω, which specifies angular change per unit of time, and wavenumber (or angular wave number) k, which represent the angular change per unit of space,

$v_{\mathrm {p} }={\frac {\omega }{k}}.$

Beats

The previous definition of phase velocity has been demonstrated for an isolated wave. However, such a definition can be extended to a beat of waves, or to a signal composed of multiple waves. For this it is necessary to mathematically write the beat or signal as a low frequency envelope multiplying a carrier. Thus the phase velocity of the carrier determines the phase velocity of the wave set.

Dispersion

In the context of electromagnetics and optics, the frequency is some function ω(k) of the wave number, so in general, the phase velocity and the group velocity depend on specific medium and frequency. The ratio between the speed of light c and the phase velocity v_p is known as the refractive index, n = c / v_p = ck / ω.

In this way, we can obtain another form for group velocity for electromagnetics. Writing n = n(ω), a quick way to derive this form is to observe

$k={\frac {1}{c}}\omega n(\omega )\implies dk={\frac {1}{c}}\left(n(\omega )+\omega {\frac {\partial }{\partial \omega }}n(\omega )\right)d\omega .$

We can then rearrange the above to obtain

$v_{g}={\frac {\partial w}{\partial k}}={\frac {c}{n+\omega {\frac {\partial n}{\partial \omega }}}}.$

From this formula, we see that the group velocity is equal to the phase velocity only when the refractive index is independent of frequency ${\textstyle \partial n/\partial \omega =0}$. When this occurs, the medium is called non-dispersive, as opposed to dispersive, where various properties of the medium depend on the frequency ω. The relation $\omega (k)$ is known as the dispersion relation of the medium.

See also

• Cherenkov radiation
• Dispersion (optics)
• Group velocity
• Propagation delay
• Shear wave splitting
• Wave propagation
• Wave propagation speed
• Planck constant
• Speed of light
• Matter wave#Phase velocity

References

Bibliography

• Crawford jr., Frank S. (1968). Waves (Berkeley Physics Course, Vol. 3), McGraw-Hill, ISBN 978-0070048607 Free online version
• Brillouin, Léon (1960), Wave Propagation And Group Velocity, New York and London: Academic Press Inc., ISBN 978-0-12-134968-4 {{citation}}: ISBN / Date incompatibility (help)
• Main, Iain G. (1988), Vibrations and Waves in Physics (2nd ed.), New York: Cambridge University Press, pp. 214–216, ISBN 978-0-521-27846-1
• Tipler, Paul A.; Llewellyn, Ralph A. (2003), Modern Physics (4th ed.), New York: W. H. Freeman and Company, pp. 222–223, ISBN 978-0-7167-4345-3